| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- gjk-epa
- unittest
- narrow-phase
- optimization
- Turtle
- mock
- ROS
- patch
- MPC
- Service
- UV
- subsribe
- namespace
- separating axis theorem(sat)
- Package
- Python
- Gradient
- convex
- 워크스페이스
- Publish
- Topic
- rospy.spin
- Turtlesim
- roslaunch
- gjk
- 비동기적
- broad-phase
- CONSTRAINTS
- remapping
- QT
- Today
- Total
똑바른 날개
Collision Detection알고리즘(Narrow-phase, Broad-phase) 본문
Collision Detection
Collision Detection은 일반적으로 Broad-Phase와 Narrow-phase로 두단계 나누어 수행한다.
Broad-phase
전체 커다란 객체들중 정밀하게 바라보아야할 객체와 무시해야될 객체를 빠르게 걸러내는 작업을 하는 단계이다.
이때 만약, 모든 객체를 brute-force(완전탐색 알고리즘) 구현한다면, 알고리즘의 복잡성은 \( O(n^2) \)이 된다. 하여, 이러한 복잡도를 사용하기 위해 다양한 알고리즘을 사용한다.
Axis-Aligned Bounding Box (AABB)
객체를 직사각형이나 직육면체로 감싸서 계산. 계산이 빠르지만, 객체가 회전하면 빈 공간이 많아질 수 있다는 단점이 존재

Oriented Bounding Box (OBB)
객체의 실제 방향에 맞춰 경계 상자를 설정하여 AABB보다 더 정확한 성능, 그러나 연산이 느려짐

Bounding Volume Hierarchies (BVH)
객체의 세부 기하정보를 트리 형태로 구성하여, 상위 레벨에서는 단순 경계체로 후보를 걸러내고 하위 레벨에서 점차 정밀한 검사를 수행합니다. FCL(Flexible Collision Library) 등 여러 라이브러리에서 사용됩니다.


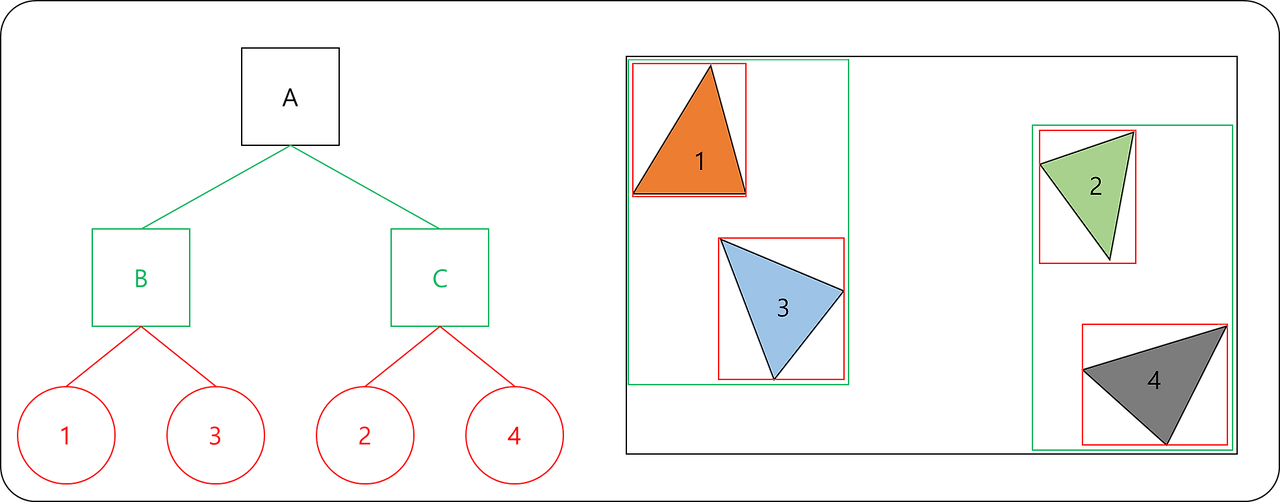
Sort and Sweep
각 객체의 바운딩 volume을 x,y,z 축중 하나의 축에 투영하여, 일차원 충돌 구간을 정의하고, 두객체의 충돌 구간이 겹치지 않는다면, 충돌할수없음을 판단한다.
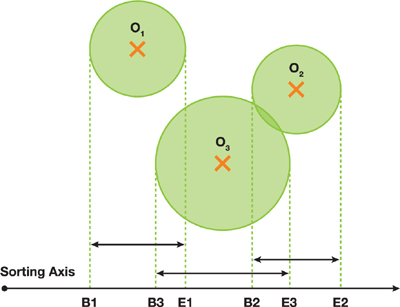
Spatial Subdivision
Spatial Subdivision은 공간을 균일한 grid로 분할한다. grid셀의 크기는 가장 큰 객체의 volume보다 크거나 같게 유지한다. 이렇게 나누어진 각셀에 두객체가 인접하거나, 같은 셀에 속할때만 충돌검사를 수행하며, 나머지는 무시한다.

객체는 총 8개의 셀과 겹칠수 있다.

o1, o2: 충돌검사
o2, o3: 충돌검사
o2, o3 : 충돌검사 x (주 객체의 중심이 셀2에 존재하지 않는다.
Narrow-phase
Broad-phase를 거친 뒤 남은 객체들은 충돌의 가능성이 있는 객체들이다. 이러한 객체들을 정밀하게 충돌하고 있는지 검증하는 것이 Narrow-phase에서 진행하는 것이다.
Separating Axis Theorem(SAT)
두 convex 객체가 서로 충돌하지 않으려면, 두 객체의 projection 결과가 겹치지 않는 분리된 축이 존재해야 한다. 모돈 분리된 축에 대해 projection 결과가 겹친다면 반드시 충돌된다.
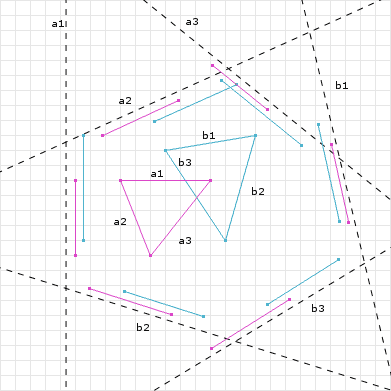
두 볼록 집합 A,B에 대해 임의의 방향벡터 d에 대한 projection은 다음과 같다.
\begin{aligned} \text{Projection}_A(\mathbf{d}) = [\min_{\mathbf{a}\in A} (\mathbf{a}\cdot \mathbf{d}), \max_{\mathbf{a}\in A} (\mathbf{a}\cdot \mathbf{d})] \\ \text{Projection}_B(\mathbf{d}) = [\min_{\mathbf{b}\in B} (\mathbf{b}\cdot \mathbf{d}), \max_{\mathbf{b}\in B} (\mathbf{b}\cdot \mathbf{d})] \end{aligned}
if any d에 대해서 두구간이 겹치지 않는다면, 즉
$$
\max_{\substack{a \in A}} \left( \min_{\substack{b \in B}} (a \cdot d), \min_{\substack{b \in B}} (b \cdot d) \right)
>
\min_{\substack{a \in A}} \left( \max_{\substack{b \in B}} (a \cdot d), \max_{\substack{b \in B}} (b \cdot d) \right)
$$
라면 d는 분리 축이며, 따라서 A와 B는 충돌하지 않는다.
GJK(Gilbert-Johnson-Keerthi)
Convex객체간의 충돌여부 판단하거나, 객체 사이의 최소 거리를 계산하기 위해 사용되는 알고리즘

Convex하지 않는 object에 경우 사용할 수 없다.
MinKowski Sum/Different
두 오브젝트의 모든 vector을 더하거나 뺐을때의 결과이다.

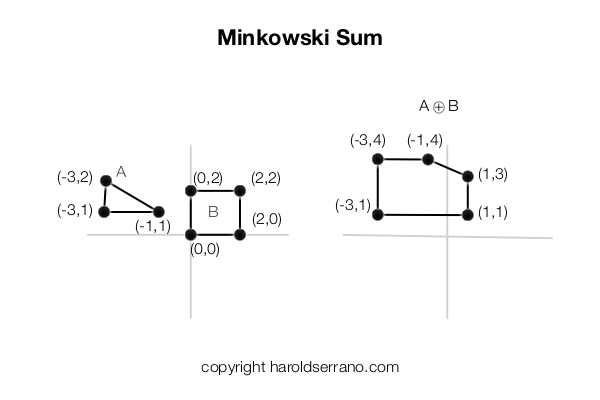
- 충돌경우
두 object가 Collision 상태라면, Minkowski Different로 만들어진 object은 원점을 포함한다. - 충돌이 발생하지 않은 경우
Minkowski Different로 만들어진 object의 simplex를 만들고 원점과의 최단거리를 근사하여, 두 객체 사이의 최소 거리를 계산할 수 있다.
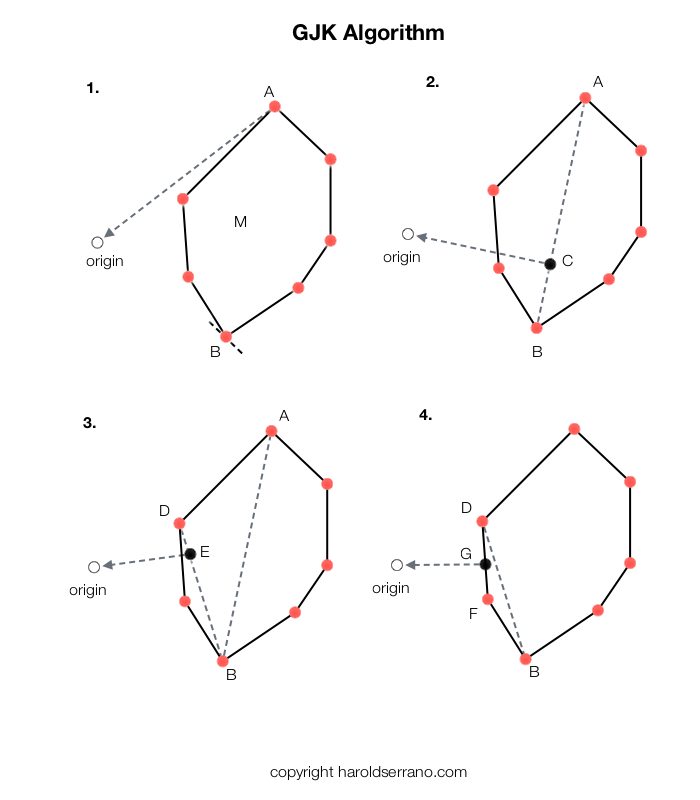
- The algorithm arbitrarily starts with the vertex A as the initial simplex in set Q, Q={A}.
- Searching for the supporting point in direction -A results in B. B is added to the Simplex set, Q={A, B}
- The point in the convex hull Q closest to the origin is C. Because both A and B are needed to express C as a convex combination, both are kept in Q.
- D is the supporting point in direction -C and it is added to Q, giving Q={A, B, D}.
- The closest point in the convex hull Q closest to the origin is now E.
- Because only B and D are needed to express E as a convex combination of vertices in Q, Q is updated to Q={B, D}. The supporting point in direction -E is F, which is added to Q.
- The point on the convex hull Q closest to the origin is now G.
- D and F are the smallest set of vertices in Q need to express G as a convex combination. Q is updated to Q={D, F}.
- At this point, because no vertex is closer to the origin in direction -G than G itself, G must be the closest point to the origin, and the algorithm terminates. No collision occurred.
GJK-EPA알고리즘
GJK 알고리즘으로 도형의 충돌판정을 알 수 있다. 그러나, 얼마나 깊게 충돌을 했는지를 알기 위해서 등장한 알고리즘이다.
EPA 동작 원리
- GJK에서 사용한 Simplex를 Polytope로 지정한다.
- 원점과 Polytope의 Edge의 거리가 가장 가까운 Edge를 고른다.
- 원점에서 가장 가까운 Edge 쪽을 가리키는 Vector를 이용해 Support Point를 구하고 Edge의 두 점 사이에 Support를 삽입해서 Polytope를 확장한다.
- Support Point가 Polytope에 포함되 있으면 확장을 중단한다.
- 이렇게 최종적으로 완성된 Polytope의 Edge중 가장 가까운 Edge와의 거리가 Depth, 원점에서 Edge 쪽 방향이 Contact normal이 된다.
| Step |
polytope원형
|
가장 가까운 Edge찾기 |
| 1 |
 |
 |
| 2 |
 |
 |
| 3 |
 |
 |
Reference
https://m.blog.naver.com/jerrypoiu/221172549241
https://mathmakeworld.tistory.com/109#google_vignette
https://blog.smilecat.dev/posts/graphics-separating-axis-theorem
https://www.slideshare.net/slideshow/collision-detection-algorithms/251207941
https://www.haroldserrano.com/blog/visualizing-the-gjk-collision-algorithm
