| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Service
- separating axis theorem(sat)
- namespace
- Turtlesim
- 비동기적
- broad-phase
- QT
- convex
- Publish
- Topic
- UV
- remapping
- optimization
- subsribe
- CONSTRAINTS
- unittest
- Package
- ROS
- MPC
- roslaunch
- narrow-phase
- gjk
- patch
- Python
- 워크스페이스
- Turtle
- gjk-epa
- mock
- Gradient
- rospy.spin
- Today
- Total
똑바른 날개
[MPC책 공부 - 14] 2장 - Linear quadratic MPC예제 본문
시스템 정의
$$
x^+ = f(x, u) := x - u
$$
즉, 다음 상태는 현재 상태에서 제어 입력을 뺀 값이다.
비용 함수
stage cost
$$
\ell(x, u) := \frac{1}{2}(x^2 + u^2)
$$
terminal cost
$$
V_f(x) := \frac{1}{2}x^2
$$
total cost(horizon =2 )
$$
V_N(x, u) = \frac{1}{2} \left( x(0)^2 + u(0)^2 + x(1)^2 + u(1)^2 + x(2)^2 \right)
$$
제어 제약 조건:
$$
u(k) \in [-1, 1] \quad \text{for } k = 0, 1
$$
두 가지 풀이 방식
방법 1: 상태와 입력 모두를 최적화 변수로 사용
구분방식 1: 상태와 입력을 모두 최적화 변수로 사용방식 2: 입력만 최적화 변수로 사용
| 구분 | 방식 1: 상태와 입력을 모두 최적화 변수로 사용방식 | 입력만 최적화 변수로 사용 |
| 변수 | \( x(0),x(1),x(2),u(0),u(1) \) | \( u(0),u(1) \) |
| 등식 제약 | \( x(0)=x_{\text{init}},\ x(1)=x(0)-u(0),\ x(2)=x(1)-u(1) \) | 없음 (상태를 직접 식에 대입함) |
| 목적 함수 | 위와 동일 | 상태를 없애고 \( x_{\text{init}} \)과 \( u \)만으로 표현 |
목적함수
$$
\frac{1}{2} \left( x(0)^2 + u(0)^2 + x(1)^2 + u(1)^2 + x(2)^2 \right)
$$
제약 조건
$$
\begin{aligned}
x(0) &= x \quad \text{(initial condition)} \\
x(1) &= x(0) - u(0) \quad \text{(system equation)} \\
x(2) &= x(1) - u(1) \\
u(0), u(1) &\in [-1, 1]
\end{aligned}
$$
이 방식은 상태와 입력을 모두 결정 변수로 다루고, 시스템 방정식은 equality constraint로 처리된다.
방법 2: 입력만 최적화 변수로 사용
이 방식은 상태들을 명시적으로 변수로 두지 않고, 시스템 방정식을 통해 상태를 계산한다.
상태는 다음과 같이 유도된다
$$
\begin{aligned}
x(1) &= x - u(0) \\
x(2) &= x - u(0) - u(1)
\end{aligned}
$$
목적 함수는 다음과 같다.
$$ \begin{aligned} V_N(x, u) &= \frac{1}{2} \left[ x^2 + u(0)^2 + (x - u(0))^2 + u(1)^2 + (x - u(0) - u(1))^2 \right] \\ &= \frac{3}{2}x^2 - 2x \cdot [1 \quad 1] u + \frac{1}{2} u^T H u \end{aligned} $$
$$
H = \begin{bmatrix}
3 & 1 \\
1 & 2
\end{bmatrix}
$$
제약 없는 최적 입력 계산
목적 함수를 \(u = [u(0), u(1)]^\top\)에 대해 미분하고 0으로 두면 다음과 같은 최적 입력이 나온다.
$$ u^\star(x) = \begin{bmatrix} \frac{3}{5}x \\ \frac{1}{5}x \end{bmatrix} $$
제약 조건
입력 제약 \(|u(k)| \le 1\)을 적용하면, 각각의 제어 입력을 [-1, 1] 범위로 잘라야 한다.
$$ \kappa_N(x) = \operatorname{sat}\left(\frac{3}{5}x\right) $$
$$ \operatorname{sat}(z) = \begin{cases} 1, & z > 1 \\ z, & -1 \le z \le 1 \\ -1, & z < -1 \end{cases} $$
최종적으로 제어 루프는 다음과 같이 된다.
$$ x^+ = x - \kappa_N(x) $$
- saturation 함수
$$ \text{sat}(z) = \begin{cases} 1 & \text{if } z > 1 \\ z & \text{if } -1 \le z \le 1 \\ -1 & \text{if } z < -1 \end{cases} $$
결과
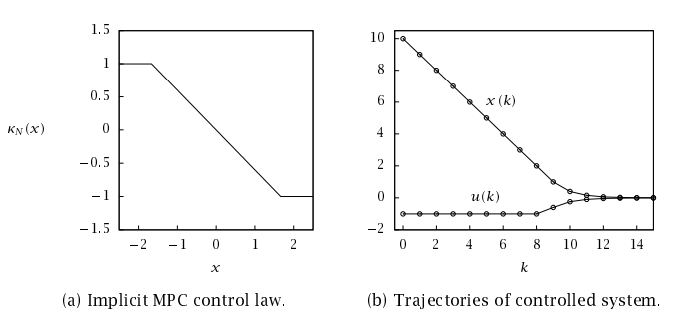
예제) 초기 상태 x = 10의 결과
1. \(u(0) = \operatorname{sat}(3 \cdot 10 / 5) = \operatorname{sat}(6) = 1\)
2. \(x(1) = 10 - 1 = 9\)
3. \(u(1) = \operatorname{sat}(3 \cdot 9 / 5) = \operatorname{sat}(5.4) = 1\)
4. \(x(2) = 9 - 1 = 8\)
총 비용:
$$ V_N(10) = \frac{1}{2}(10^2 + 1^2 + 9^2 + 1^2 + 8^2) = 124 $$
또한 해당 시스템은 시간에 따라 시스템의 변화가 생기는 구조가 아니다.즉, Time-invariant하다.
다시 정리해보면,
$$ x^+ = x + \kappa_N(x), \quad \kappa_N(x) = -\text{sat}\left(\frac{3x}{5}\right) $$
Python 코드로 구현
import numpy as np
import matplotlib.pyplot as plt
def sat(z):
return np.clip(z, -1, 1)
def kappa_N(x):
return sat(3*x/5)
# 초기 상태
x0 = 10
horizon = 14
x = x0
x_traj = [x]
u_traj = []
# 시뮬레이션 (horizon 길이만큼)
for _ in range(horizon):
u = -kappa_N(x)
u_traj.append(u)
x = x + u
x_traj.append(x)
k = np.arange(horizon + 1)
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# (a) Optimal control law
xs = np.linspace(-10, 10, 401)
axs[0].plot(xs, kappa_N(xs))
axs[0].set_title('Optimal Control Law')
axs[0].set_xlabel('x')
axs[0].set_ylabel(r'$\kappa_N(x)$')
axs[0].axhline(0, color='black', lw=0.5, ls='--')
axs[0].axvline(0, color='black', lw=0.5, ls='--')
axs[0].axhline(1, color='red', lw=0.5, ls='--')
axs[0].axhline(-1, color='red', lw=0.5, ls='--')
axs[0].set_xlim(-10, 10)
axs[0].set_ylim(-2, 2)
axs[0].set_xticks(np.arange(-10, 11, 2))
axs[0].set_yticks(np.arange(-2, 3, 1))
axs[0].grid(True)
# (b) State and input trajectories
axs[1].plot(k, x_traj, marker='o', label=r'$x(k)$')
axs[1].plot(k[:-1], u_traj, marker='s', label=r'$u(k)$')
axs[1].set_title(r'State and Control Input Trajectories ($x_0 = 10$)')
axs[1].set_xlabel('Time step k')
axs[1].grid(True)
axs[1].legend()
plt.tight_layout()
plt.show()
'제어 > mpc' 카테고리의 다른 글
| [MPC책 공부 - 13] 2장 - 최적 제어의 해는 언제 존재하는가? (0) | 2025.04.01 |
|---|---|
| [MPC책 공부 - 12] 2장 - 시스템 연속성, 제약, 비용 함수 (0) | 2025.03.25 |
| [MPC책 공부] 2장도입, 표기법 정리 (0) | 2025.03.24 |
| [MPC책 공부 - 11] 외란과 보정 Disturbances and Zero offset (0) | 2025.03.23 |
| [MPC책 공부 - 10] Tracking (0) | 2025.03.21 |


